QUESTION
1. Diffusion-limited association rate.
(a) Find the (diffusion-limited) association rate constant k for a 3 nm diameter transcription factor protein to bind a 25 bp DNA target via unrestricted three-dimensional diffusion.
(b) Use (a) to find the time needed for the protein to bind one target located somewhere inside an E. coli cell.
(c) Find the time needed for the protein of (a) to bind one target located somewhere inside human nucleus, assuming that it starts somewhere in the nucleus.
2. Facilitated diffusion and compartments.
(a) A protein of diameter d is synthesized in a cell of diameter dcell. Find a simple formula for the time required for the protein to bind to any one of the N nuclear pores of diameter p on the nuclear envelope via three-dimensional diffusion.
Hint: the more pores means shorter times, you put the pore number N appropriately either in the nominator or denominator of the equation that we discussed in the classroom.
(b) Suppose the protein of (a), following binding to a nuclear pore, is immediately and irreversibly transported into the nucleus of diameter dnucl . Estimate the time required for that protein to find its target of size b inside the nucleus.
(c) Now, suppose there had been no nucleus or nuclear pores, so that the protein would have had to find its target by searching the entire cell volume. Estimate the time required, and compare to the sum of (a) and (b).
(d) What is the condition so that the nuclear pore strategy saves time?
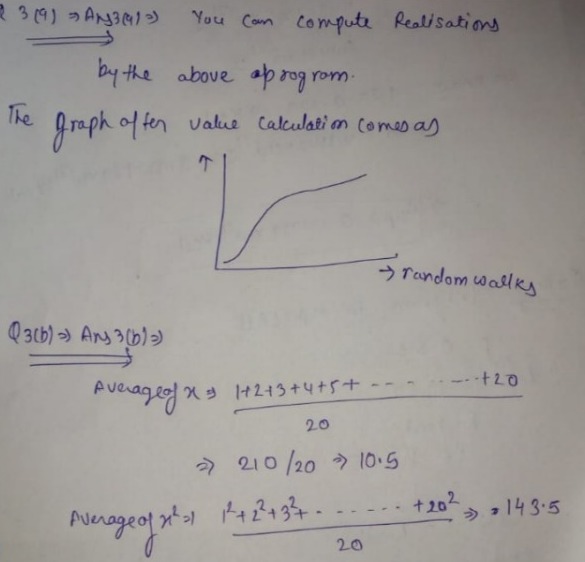
3. Write a computer program to compute random walks in one dimension (along one coordinate) where the steps are ±1 with 50% probability. You are free to use your favorite computer language (our official choice is Matlab).
(a) Compute and plot 10 realizations (basically 10 independent walks run with different random number seeds) of N=100 walks and plot (you could put them all on one plot, or on separate plots).
(b) Now, compute average (mean) final values of x and x2 , as well as the standard error in those quantities, averaging over at least 20 independent realizations for each of N=20, 50, 100, 200, 500, 100 steps.
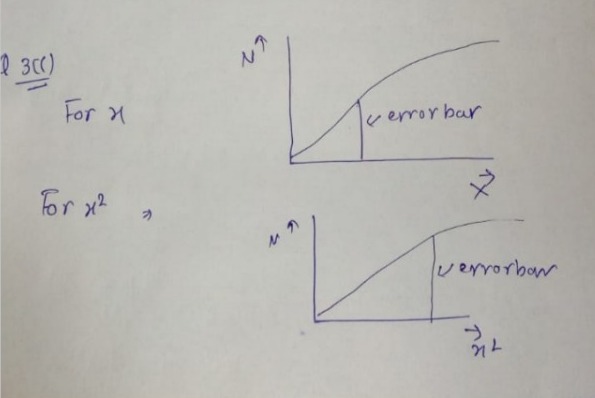
(c) Plot the mean final values of x and x2 (b) including error bars, versus N to estimate the diffusion coefficient, in units (step units)2 / (time step) ?
ANSWER
Answer 1



Answer 2



Answer 3

Looking for best Bio-Physics Assignment Help. Whatsapp us at +16469488918 or chat with our chat representative showing on lower right corner or order from here. You can also take help from our Live Assignment helper for any exam or live assignment related assistance