QUESTION
Problem Set 1

4.4 Questions 6 and 12 only:



7.1 Questions 2, 6, and 20 only:


7.2 Questions 3 and 6 only:

7.3 Questions 3 and 43 Only:



Problem Set 2
8.1 Questions 3 and 10 only:


8.2 Questions 3, 5, 21, 29 Only:



8.3 Question 5 only:
8.4 Questions 2 and 7 only:

8.5 Question 3 only:

Section 8.4, page 410, exercise 3
ANSWER
Set 1
Ex 4.4-
6) for n=5,
walk(5)
- Start
- n!=1 and n!=2
- return
- walk(4) + walk (3)
- walk (4)
- n!=1 and n!=2
- return
- walk(3) + walk(2)
- walk(3)
- n!=1 and n!=2
- return
- walk(2) + walk (1)
- walk(2)
- n!=1 but n=2
- return 2 to line 12
- walk(3)=2+1=3 return 3 to line 8
- walk(4)=3+2=5 return 5 to line 4
- walk(5)=5+3=8
- return 8
- Stop
12) If there is single element, return it.
Else return minimum of following.
a) Last Element
b) Value returned by recursive call
for n-1 elements.
int findminimum(int S[], int n)
{ if (n == 1)
return S[0];
return min(S[n-1], findminimum(S, n-1));
}
Proof by mathematical induction:
Base case: for n=1, let Sn={2}
As n=1, S0=2 is returned, hence true for n=1.
Now, suppose, for n=k, let the minimum element be ‘m’, then for n=k+1, say if one more element ‘o’ is added, the last element will be ‘o’ and now min(o,m) will be returned, hence proved.
Ex 7.1
2) Given sequence: 3,6,9,15,24,39,……
The recurrence relation: an=an-1+an-2
Initial conditions: a0=3, a1=6.
6) P= $2000, r=0.14, An=P(1+r)n;
A1=(2000(1+0.14)1)=2280;
A2=(2000(1+0.14)2)=2599.2;
A3=(2000(1+0.14)3)=2963.088.
20) The sequence satisfies the recurrence relation Sn+1=Sn+Sn-1, with initial conditions, S1=2, S2=3.
To show that Sn=fn+1 , n=1,2,……, where f denotes the Fibonacci sequence, we will use induction.
The base case where n=1, S1=f1+1=f2=2 and n=2, S2=f2+1=f3=3 is true.
Now, suppose Sk=fk+1 for all k<n, where n>=3;
We see that for: Sk+1= Sk+Sk-1=fk+1+fk=fk+2.
Hence proved.
Ex 7.2-
3) No, an=2nan-1 is not a linear homogeneous recurrence relation with constant coefficients as the coefficients is 2n which is not constant.
6) Yes, an=7an-2-6n-3 is a linear linear homogeneous recurrence relation with constant coefficients. The order of the relation is 2.
Ex 7.3-
3) For sequence, sn={‘C’,’G’,’J’,’M’,’X’}
To find if ‘C’ is in the sequence or not.
START
i<j //i=1, j=5, key=’C’, n=5.
k=(i+j)/2 = 3
sk=s3=’J’
key!=sk or 3
key<sk or 3 //search left half
j=k-1=3-1=2
i<j //i=1,j=2,key=’C’,n=5.
k=(i+j)/2 = 1
sk=s1=’C’
key=sk or 1 //found.
Stop
43)
bn=the number of multiplications in line 5 required for compute an.
Using mathematical induction,
When, n=1, b1=0
When, n=k, we can see that the multiplication will be performed for every integers from k till 1, for 1 bk=0, so bk for k, will be k-1 (excluding the case of 1).
Similarly, for n=k+1, bk+1=bk+1(as only one interger increment is there so bn will only increase by 1)
bk+1=k-1+1=k.
Hence proved.
bn=n-1.
Set 2
Ex 8.1
Solution 3:
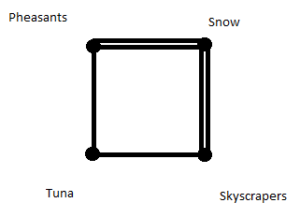
It is a kind of undirected (cyclic) graph because here we need to show no. of games played between the teams only.
Solution 10: Path from a to a that passes through each edge exactly one time is a→ b→ c→ e→ b→ d→ e→ f→ c→ a .
Ex 8.2
Solution 3:
- A simple path
Solution 5:
- A cycle

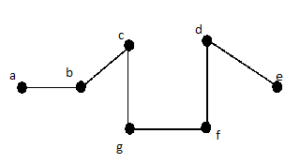
Solution 21:
Simple paths:
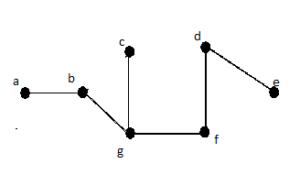
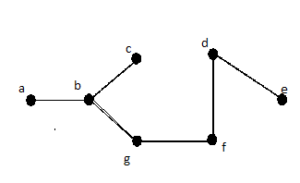

Solution 29 :
Above graph has an Euler cycle. Because it has all vertices with non-zero degree are connected and all vertices have even degree.
Euler cycle: a→b→f→g→j→h→i→e→j→f→e→d→b→c→d→i→c→h→a
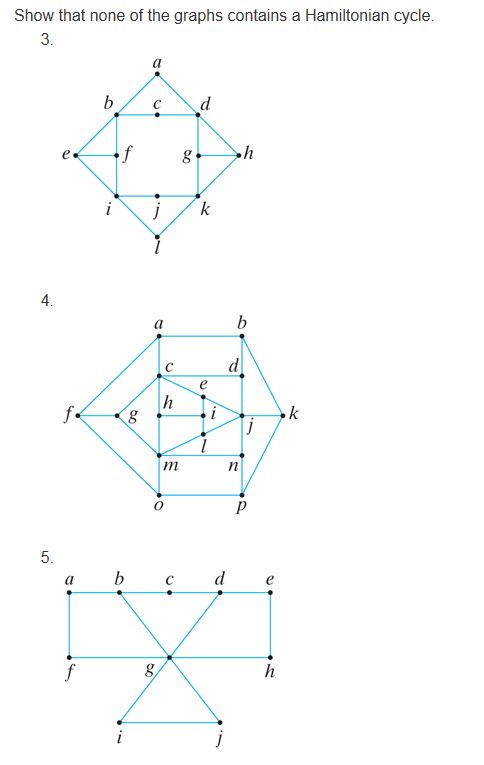
Ex 8.3
Solution 5:
Lemma: if G is a graph having Hamiltonian cycle then for every non-empty subset S⊆ V(G) ,
C(G-S)<=|S|. where C(G-S) is the no. of connected components after removal of S subset and |S| is cardinality of set S.
Since it is a necessary condition for having Hamiltonian cycle.
Here,
V(G)={a,b,c,d,e,f,g,h,i,j}
Let S={g}
|S|=1 and C(G-S)=2
Since it doesn’t hold the necessary condition i.e. C(G-S)<=|S|.
Hence, given graph G doesn’t have Hamiltonian cycle.
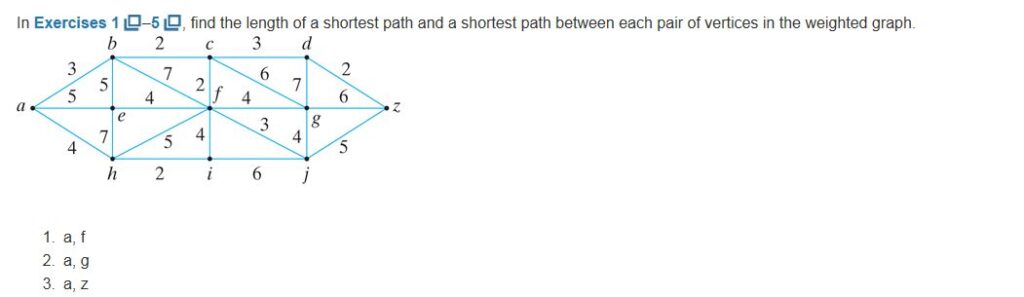
Ex 8.4
Solution 2:
Shortest path from a to g : a→b→c→g with length=3+2+6=11
a→b→c→f→g with length =3+2+2+4=11
Solution 7:
Algorithm Steps:
1. Make an empty set of shortest path tree that will contain all shortest paths.
2. Initially set all length values as ∞. Allocate length value equals to 0 for the source vertex.
3. While set does not contain all the vertices repeat step4 and step5.
4. Choose a vertex u that does not belong to the set and has a minimum length value and include it in the set.
5. update length value of all the adjacent vertices of u by checking through all the adjacent vertices. For every adjacent vertex v, if total of length value from source and length of edge (u-v), is smaller than length value of v, then amend the length value of v.
Ex 8.5
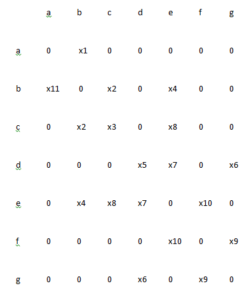
Solution 3: adjacency matrix is given as follows:
Looking for best Mathematics Assignment Help. Whatsapp us at +16469488918 or chat with our chat representative showing on lower right corner or order from here. You can also take help from our Live Assignment helper for any exam or live assignment related assistance.