Discrete Mathematics Practical Solution Sample

QUESTION

Lesson 1

Exercise-1.1

•Section 1.1, page 12, problems 15, 53.

In Exercises 1–16, let the universe be the set U={1, 2, 3, …, 10}.U={1, 2, 3, …, 10}.Let A={1, 4, 7, 10}, B={1, 2, 3, 4, 5},A={1, 4, 7, 10}, B={1, 2, 3, 4, 5},and C={2, 4, 6, 8}.C={2, 4, 6, 8}. List the elements of each set.

A∩B∪C

In Exercises 52–59, draw a Venn diagram and shade the given set.

A – B

•Section 1.2, page 19, problems 21, 30.

Given that proposition p is false, proposition q is true, and proposition r is false, determine whether each proposition in Exercises 17–22 is true or false.

¬(p∨q)∧(¬p∨r)¬(p∨q)∧(¬p∨r)

Write the truth table of each proposition in Exercises 23–30.

¬(p∧q)∨(¬q∨r)

•Section 1.3, page 30, problem 72 only.

For each pair of propositions P and Q in Exercises 63–72, state whether or not P≡Q.P≡Q.

P=(s→(p∧¬r))∧((p→(r∨q))∧s), Q=p∨t

•Section 1.4, pages 35–36, problems 21, 28.

Determine whether each argument in Exercises 20–24 is valid.

p→q¬q∴¬pp→q¬q∴¬p

For each argument in Exercises 27–29, tell which rule of inference is used.

If fishing is a popular sport, then lacrosse is wildly popular in California. Fishing is a popular sport. Therefore, lacrosse is wildly popular in California.

•Section 1.5, pages 48–49, problems 36, 74.

Let P(x) denote the statement “x is taking a math course.“ The domain of discourse is the set of all students. Write each proposition in Exercises 32–37 in words.

¬(∀xP(x))¬(∀xP(x))

What is the literal meaning of each statement in Exercises 61–71? What is the intended meaning? Clarify each statement by rephrasing it and writing it symbolically.

Analyze the following comments by film critic Roger Ebert: No good movie is too long. No bad movie is short enough. Love Actually is good, but it is too long.

•Section 1.6, page 55, problems 24, 28.

In Exercises 22–27, T2(x, y)T2(x, y) is the propositional function “x is taller than or the same height as y.” Write each proposition in Exercises 22–25 in words.

∃x∀yT2(x, y)∃x∀yT2(x, y)

In Exercises 28–33, T3(x, y)T3(x, y) is the propositional function “if x and y are distinct persons, then x is taller than y.” Write each proposition in Exercises 28–31 in words.

∀x∀y T3(x, y)∀x∀y T3(x, y)

•Section 11.1, page 537, problem 11.

In Exercises 10–14, find the value of the Boolean expressions for

x1=1×1 = 1, x2=1×2 = 1, x3=0x3 =, x4=1×4 = 1.

(x1∧¯x2)∨(x1∨¯x3)(x1∧x¯2)∨(x1∨x¯3)

•Section 11.2, pages 548–549, problem 2.

Show that the combinatorial circuits of Exercises 1–5 are equivalent.

Lesson 2

•Section 3.1, pages 125–126, problems 21, 63.

•Section 3.2, pages 137–140, problems 27, 148.

•Section 3.3, page 150, problem 31.

•Section 3.4, page 156, problems 2, 12.

•Section 3.5, pages 163–164, problems 3, 10.

•Section 3.6, page 169, problem 12.

Lesson 3

Section 6.1, pages 264–265, problems 2, 38.

Section 6.2, page 278, problems 12, 40.

Section 6.3, page 288, problem 2.

Section 6.5, page 299, problems 2, 6, 16, 21.

Section 6.6, pages 311–312, problems 2, 15, 29, 58.

ANSWER

Lesson 1

•Section 1.1, page 12, problems 15, 53.

A∩B∪C = (A∩B)∪(A∩C)

={1,4}∪{4}

={1,4}

In Exercises 52–59, draw a Venn diagram and shade the given set.

A – B

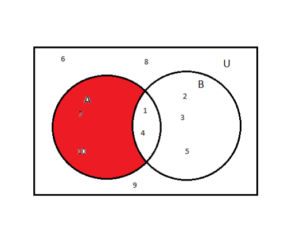
•Section 1.2, page 19, problems 21, 30.

Given that proposition p is false, proposition q is true, and proposition r is false, determine whether each proposition in Exercises 17–22 is true or false.

¬(p∨q)∧(¬p∨r)¬(p∨q)∧(¬p∨r)

Putting, F for false and T for true in the above equation, we get,

=¬(F∨T)∧(¬F∨F)¬(F∨T)∧(¬F∨F)

=¬(T)∧(T∨F)¬(T)∧(T∨F)

=F∧(T).(F)∧(T)

=F.F

=false

Write the truth table of each proposition in Exercises 23–30.

¬(p∧q)∨(¬q∨r)

p	q	r	p∧q	¬(p∧q)	¬q	(¬q∨r)	¬(p∧q)∨(¬q∨r)
F	F	F	F	T	T	T	T
F	F	T	F	T	T	T	T
F	T	F	F	T	F	F	T
F	T	T	F	T	F	T	T
T	F	F	F	T	T	T	T
T	F	T	F	T	T	T	T
T	T	F	T	F	F	F	F
T	T	T	T	F	F	T	T

•Section 1.3, page 30, problem 72 only.

For each pair of propositions P and Q in Exercises 63–72, state whether or not P≡Q.P≡Q.

P=(s→(p∧¬r))∧((p→(r∨q))∧s), Q=p∨t

Question not clear!!

•Section 1.4, pages 35–36, problems 21, 28.

Determine whether each argument in Exercises 20–24 is valid.

p→q¬q∴¬pp→q¬q∴¬p

Validating using truth table

p	q	p→q	¬q	p→q ¬q	¬p
F	F	T	T	T	T
F	T	T	F	F	T
T	F	F	T	F	F
T	T	T	F	F	F

Not equal, hence not valid.

For each argument in Exercises 27–29, tell which rule of inference is used.

If fishing is a popular sport, then lacrosse is wildly popular in California. Fishing is a popular sport. Therefore, lacrosse is wildly popular in California.

p→q

——-

∴q

Where, p is fishing in popular sport, q is lacrosse is widely popular in California

Name of the rule of inference is Modus Ponens.

•Section 1.5, pages 48–49, problems 36, 74.

Let P(x) denote the statement “x is taking a math course.“ The domain of discourse is the set of all students. Write each proposition in Exercises 32–37 in words.

¬(∀xP(x))¬(∀xP(x))
No students (x) are taking a math course P(x).

What is the literal meaning of each statement in Exercises 61–71? What is the intended meaning? Clarify each statement by rephrasing it and writing it symbolically.

Analyze the following comments by film critic Roger Ebert: No good movie is too long. No bad movie is short enough. Love Actually is good, but it is too long.

If “x” is a “good movie” and P(x) is a movie that can’t be too long, then “no good movie is too long” can be represented as ∀xP(x)

For the last sentence, he disapproves his own quote.

•Section 1.6, page 55, problems 24, 28.

In Exercises 22–27, T2(x, y)T2(x, y) is the propositional function “x is taller than or the same height as y.” Write each proposition in Exercises 22–25 in words.

∃x∀yT2(x, y)∃x∀yT2(x, y)

There exist a x for all y such that x is taller than or the same height as y.

In Exercises 28–33, T3(x, y)T3(x, y) is the propositional function “if x and y are distinct persons, then x is taller than y.” Write each proposition in Exercises 28–31 in words.

∀x∀y T3(x, y)∀x∀y T3(x, y)

For all x and for all y, x is taller than y if x and y are distinct persons.

•Section 11.1, page 537, problem 11.

In Exercises 10–14, find the value of the Boolean expressions for

x1=1×1 = 1, x2=1×2 = 1, x3=0x3 =, x4=1×4 = 1.

(x1∧¯x2)∨(x1∨¯x3)(x1∧x¯2)∨(x1∨x¯3)

x1=1

x2=1

x3=0

x4=1

Putting the following values in the above equation, we get

=(1∧0) ∨(1∧1)(1∧0)∨(1∨1)

=(0)∨(1)(0)∨(1)

=0∨0∨1

=0∨1

•Section 11.2, pages 548–549, problem 2.

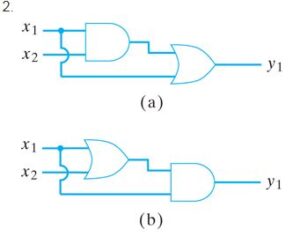
Show that the combinatorial circuits of Exercises 1–5 are equivalent.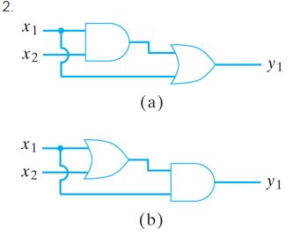

Ans. Transforming given circuit (a), into expression, we get,

y₁=(x₁.x₂)+x₁—–equation (I)

Similarly for circuit (b),

y₁=(x₁+x₂).x₁—–equation (II)

Now, taking equation (I)

y₁=(x₁.x₂)+x₁

y₁=(x₁+x₁).(x₂+x₁) (using And Distributive Law)

y₁=x₁.(x₂+x₁)(using Idempotent Law, A+A=A)

y₁=(x₁+x₂).x₁(using Commutative Law)

Above equation is equivalent to equation (II).

Hence proved.

Lesson 2

•Section 3.1, pages 125–126, problems 21, 63.

Ans. f(n) =2n

For a and b, if,

f(a) =f(b)

Implies, 2a=2b; hence, a=b

So, for function with f(a) =f(b), implying a=b, it is one-to-one also the function when plotted passes both the horizontal and vertical line tests, (i.e. No horizontal or vertical lines parallel to x and y axis crosses the curve of f(n) more than once) , which means f(n) is a one-to-one function.

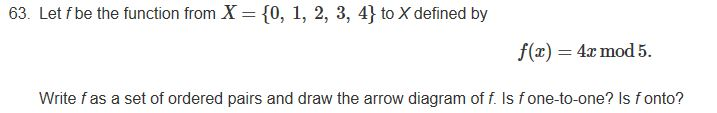
Ans.(x, f(x)) ={(0,0),(1,4),(2,3),(3,2),(4,1)}

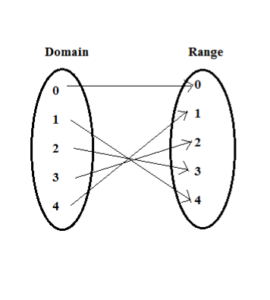
By referring the arrow diagram, we can say that f is one-to-one as each element from the domain maps to at most one element in the range.

•Section 3.2, pages 137–140, problems 27, 148.

Ans. v_n=n! +2, n>=1

v₁=1!+2=1+2=3,

v₂=2!+2=1×2 +2=4,

Similarly, v₃=3!+2=8, v₄=4!+2=26,v₅=5!+2=122,

Now, v={3,4,8,26,122,……}

Hence, we can see that v is increasing.

Ans. All the substring of string aabaabb are as follows :

“aabaabb”, “aabaab”, “abaabb”, “aabaa”, “abaab”, “baabb”, “aaba”, “abaa”, “baab”, “aabb”, “aab”, “aba”, “baa”, “abb”, “aa”, “ab”, “ba”, “bb”, “a” and “b”.

•Section 3.3, page 150, problem 31.

Ans31. Given, Relation: R= (x,y) €R if 3 divides x-y, where x and y are set of positive integers, I.

Reflexive-A relation R on a set I is reflexive if (x,x) is in R for all x in I.

Let, (a,a) be a pair where a belongs to I

Now, a-a = 0

And,.0/3=0

Hence, 3 divides the difference of all such pairs,

Therefore, R is reflexive as all (x,x) pairs, where x belongs to I.

Symmetric-A relation R is symmetric if (x,y) is in R whenever (y,x) is.

Let, (a,b) is in R

Therefore, (a-b) is divisible by 3, hence (a-b) =3k

Now, for (b,a) to be in R, B-a should also be divisible by 3,

(b-a) = – (a-b) = – 3k, which is divisible by 3,hence all such pairs are in R.

Therefore, R is symmetric.

Antisymmetric-A relation R is antisymmetric if the only way that both (x,y) and (y,x) can be in R, if x=y.

The above relation is not antisymmetric.

Transitive-A relation R is transitive if (x,y) in R and (y,z) in R implies (x,z) in R.

Let, (a,b) and (b,c) be two pairs with a, b and c belong to I.

Therefore, a-b is divisible by 3, hence,let a-b = 3k and similarly b-c is also divisible by 3, and let b-c =3k’

Now, for pair (a,c), a-c = a-b+b-c =(a-b)+(b-c) =3k+3k’ = 3(k+k’), which is also divisible by 3

Therefore, all such pairs are in R, hence R is transitive.

Partial order-A partial order is a relation, that is reflexive, transitive and antisymmetric. Therefore relation R is not Partial order.

•Section 3.4, page 156, problems 2, 12.

Ans2. For a relation to be equivalence, it should be reflexive, symmetric, and transitive.

R={(1,1),(2,2),(3,3),(4,4),(5,5),(1,3),(3,1),(3,4),(4,3)}

(I). Reflexive – all the (a,a) pairs are in R for all a belongs to {1,2,3,4,5}, hence R is reflexive.

(II). Symmetric – all the (a,b) pairs in relation R have a symmetrical (b,a) pairs in R, hence R is symmetric.

(III). Transitive – not for all (a,b) pairs and (b,c) pairs in relation R, there is a (a,c) pair, hence R is not transitive.

Example, for (1,3) and (3,4), there is no (1,4) pair.

Ans12. The relative is reflexive

It is transitive as (x,y) lives in the same country at one time and in the same time (y,z) have to live there as y is in both the pairs, hence (x,z) must be in the relation.

It is symmetric as if x and y lives in the country then y and x lives in the country.

Hence, the relation is an equivalence relation.

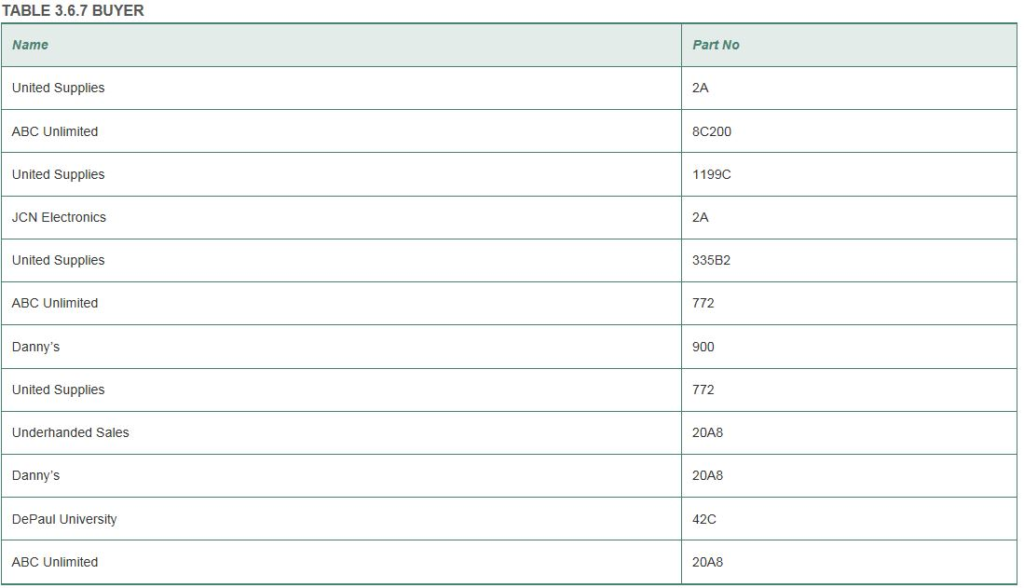
•Section 3.5, pages 163–164, problems 3, 10.

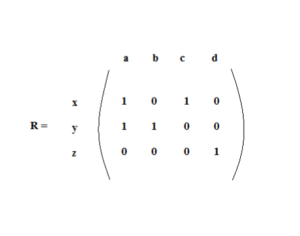
Ans3. The matrix of the relation R from X: x, y, z to Y: a, b, c, d is,

Ans10. The relation R, as a set of ordered pairs,

R={ (w,w), (w,y) , (y,w) , (y,y) , (z,z) }

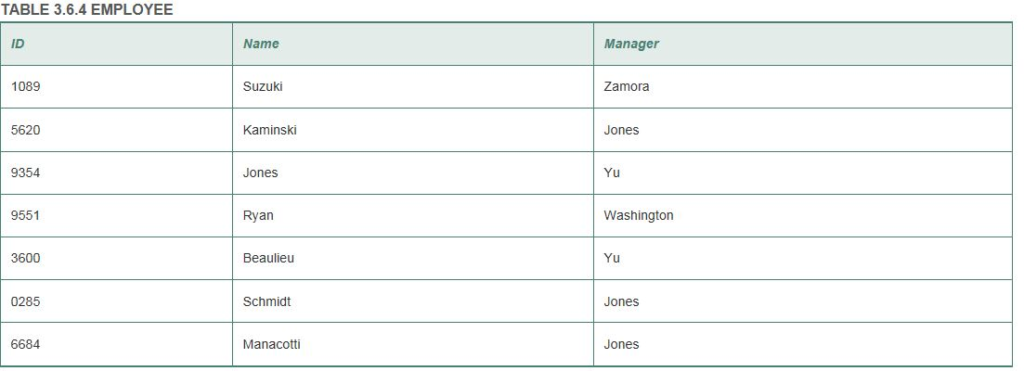
•Section 3.6, page 169, problem 12.

Lesson 3

Section 6.1, pages 264–265, problems 2, 38.

Ans2. Using multiplication principle of counting, the number of dinners at Kay’s Quick Lunch consisting an optimal appetizer, one main course, and an optimal beverage will be 4. We can also verify this by making a tree diagram.

Ans38. 2⁶, as two bits are fixed to be one we only have 6 places to be filled by 0 and 1 which can be done by 2⁶ ways.

Section 6.2, page 278, problems 12, 40.

Ans12. The number of strings can be formed by ordering the letters ABCDE containing the substrings DB and AE will be 3! or 6.

Ans40. 8!/(3!5!) or 54

Section 6.3, page 288, problem 2.

Ans2. SCHOOL has repeating Os, hence the total number of strings that can be formed by ordering the letters of SCHOOL will be 6!/2! or 360.

Section 6.5, page 299, problems 2, 6, 16, 21.

Ans2. When a coin is tossed either Head(H) or Tail(T) may occur and when a die is thrown the numbers from 1 to 6 may occur.

∴ The sample space for the event will be,

S= {H1, H2, H3, H4, H5, H6

T1, T2, T3, T4, T5, T6}

And the list of the members of the event “the die shows an odd number” are:

{H1, H3, H5, T1, T3, T5}

Ans6. The sample space for the problem will be

S= {11,12,13,14,15,16

21,22,23,24,25,26

31,32,33,34,35,36

41,42,43,44,45,46

51,52,53,54,55,56

61,62,63,64,65,66}

The list of members of the event “doubles occur” are:

{11,22,33,44, 55,66}

Ans16. Total number of card in a deck = 52

Number of favourable outcomes = 52

Number of hearts in a deck of 52 cards= 13

Therefore, the probability os the selected card to be ‘a heart’ is

P(A) = Number of favourable outcomes/Total number of possible outcomes = 13/52=¼

Ans21. Total number of ways to select four microprocessors out of 100 microprocessors are C(100,4)

Number of ways to select 4 microprocessors with exactly one defective microprocessor are C(90,3) C(10,1).

So, P(E)=(C(10,1)*C(90,3))/C(100,4)

Section 6.6, pages 311–312, problems 2, 15, 29, 58.

Ans2. P(2)=⅛, can be seen in the example.

Similary, P(4)=⅛ and P(6)=⅛

So, probability of getting an even number is P(2)+P(4)+P(6)=⅜

Ans15. Given, P(2)=P(4)=P(6) and P(1)=P(3)=P(5)=3(P(2))

Since, 1=P(1)+P(2)+P(3)+P(4)+P(5)+P(6)

3P(2)+3P(1)

3P(2)+3(3(P(2)))

12P(2)

Therefore, P(2)=1/12

P(1)=3/12=¼

Two dice are rolled, the list of members of the event of getting a sum of 7 are {(1,6),(2,5),(3,4),(4,3),(5,2),(6,1)}

Now, probability of getting a 1 and a 6 is 1/4 × 1/12 = 1/48

Total probability of the event is 6×1/48 = ⅛

Ans29. Probability of a boy to be born= probability of a girl to be born= P(B)= P(G)= ½

There can be 2⁴=16 possibilities of child.

The chances of having exactly 2 girls are calculated as n!/(k!(n−k)!) = 4!/(2!2!) = 6

Therefore, the probability of getting exactly 2 girls is 6/16 = ⅜

Ans58. Here, we can refer to Bayes’ theorem,

If having a headache is represented by “H”, and having a fever is represented by “F”, then according to Bayes’ theorem, P(H/F)=(P(F/H) × P(H)) /P(F)

Now, P(F) = 0.02

P(H)) = 0.01

P(F/H) = 0.4

Now, P(H/F) = (0.4×0.01)/0.02 = 0.2

Looking for best Mathematics Assignment Help. Whatsapp us at +16469488918 or chat with our chat representative showing on lower right corner or order from here. You can also take help from our Live Assignment helper for any exam or live assignment related assistance.