Inferences from two samples using the process of Hypothesis Testing

QUESTION

 

 

ANSWER

 

HYPOTHESIS TESTING

We have a dataset. We want to test the claim that the mean BMI of men is equal to women.( μ₁₌ Mean BMI of female_, μ₂₌ Mean BMI of male)

We assume that the 2 samples are independent simple random samples selected from normally distributed populations. We don’t assume the population standard deviations are equal.

The test procedure, called the two-sample t-test, is appropriate when the following conditions are met:

• The sampling method for each sample is simple random sampling.
• The samples are independent.
• The sampling distribution is approximately normal.
• The sample size is greater than 40, without outliers.

We checked for outliers. The female dataset has 1-2 outliers and male dataset has 3-4 outliers. Since they are deviating slightly we have ignored the values. As sample size is large we proceed with a formal hypothesis test.

State the Hypotheses

Every hypothesis test requires the analyst to state a null hypothesis and an alternative hypothesis. The hypotheses are stated in such a way that they are mutually exclusive. That is, if one is true, the other must be false; and vice versa.

The table below shows three sets of null and alternative hypotheses. Each makes a statement about the difference d between the mean of one population μ₁ and the mean of another population μ₂. (In the table, the symbol ≠ means ” not equal to “.)

Set	Null hypothesis	Alternative hypothesis	Number of tails
1	μ1 – μ2 = d	μ1 – μ2 ≠ d	2
2	μ1 – μ2 > d	μ1 – μ2 < d	1
3	μ1 – μ2 < d	μ1 – μ2 > d	1

 

The first set of hypotheses (Set 1) is an example of a two-tailed test, since an extreme value on either side of the sampling distribution would cause a researcher to reject the null hypothesis. The other two sets of hypotheses (Sets 2 and 3) are one-tailed tests, since an extreme value on only one side of the sampling distribution would cause a researcher to reject the null hypothesis.

When the null hypothesis states that there is no difference between the two population means (i.e., d = 0), the null and alternative hypothesis are often stated in the following form.

H_o: μ₁ = μ₂

H_a: μ₁ ≠ μ₂

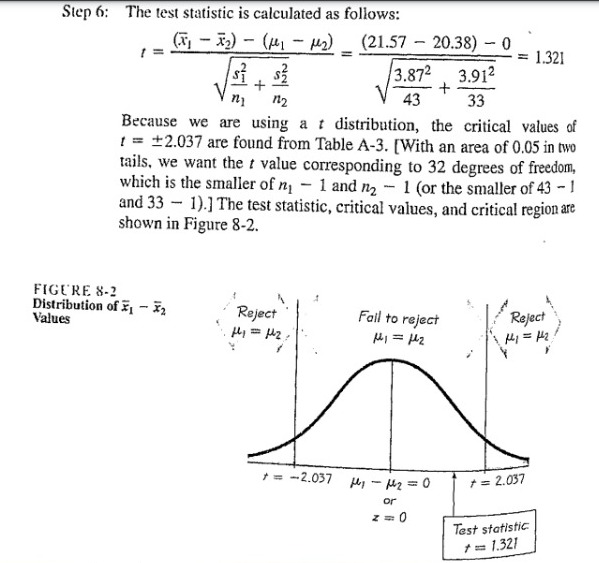
We will use as given in set 1. Because we have 2 independent samples and we are testing a claim about the 2 population means we use a t distribution with the following test statistic:

Since sample sizes are large we use normal approximation, instead of t we will have z in the above formula which will follow a N(0,1) distribution instead of t distribution.

Conclusion:

Since z value is 1.963146>1.96(significance value at 5%) null hypothesis may be rejected at 5% level of significance and we may conclude there is significant difference between sample means. So mean BMI of women is different from men.

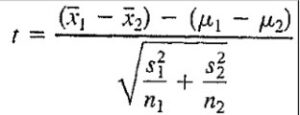
NOTE: The test is a 2 sample t test only since the sample size is (147 and 153) we cannot apply the 2 sample t test.We will instead use a normal approximation (and compare Z value with significance value at 5% level of significance).Calculated value of z statistic is correct.no need to recalculate. Have done entire experiment in excel.

As p value is 0.058081,this means that if the average BMI of all men are the same as average BMI of all women,the chance of getting this high a z score in a sample is only 0.058 or 5.8%.