QUESTION
1. Westside Auto purchases a component used in the manufacture of automobile generators directly from a supplier. Westside’s generator production operation, which is operated at a constant rate, will require 1000 components per month throughout the year (12,000 total units annually). Assume that the ordering costs are $25 per order, the unit cost is $2.50 per component, and annual holding costs are 20% of the value of inventory. Westside has 250 working days per year and a lead time of 5 days. Please report out the following information:
a) (2 pts) What is the EOQ for this component?
b) (2 pts) What is the reorder point?
c) (2 pts) What is the cycle time?
d) (4 pts) What are the total annual holding and ordering costs associated with your recommended EOQ?
Now, suppose Westside Auto decides to operate with a backorder inventory policy. Backorder costs are estimated to be $5 per unit per year. Identify the following:
e) (2 pts) Minimum cost order quantity
f) (2 pts) Maximum number of backorders
g) (2 pts) Maximum inventory
h) (2 pts) Cycle time
i) (4 pts) Total annual cost
(2 pts) Which approach would you recommend to Westside Auto, using back orders or not? Why?
2. Wilson Publishing Company produces books for the retail market. Demand for a current book is expected to occur at a constant annual rate of 7200 copies. The cost of one copy of the book is $14.50. The holding cost is based on an 18% annual rate, and production setup costs are $150 per setup. The equipment on which the book is produced has an annual production volume of 25,000 copies. Wilson has 250 working days per year, and the lead time for a production run is 15 days. Use the production lot size model to compute the following:
a) (2 pts) Minimum cost production lot size
b) (2 pts) Number of production runs per year
c) (2 pts) Cycle time
d) (2 pts) Length of a production run
e) (2 pts) Maximum inventory
f) (6 pts) Total annual cost
g) (2 pts) Reorder point
ANSWER
1. Westside Auto
a) What is the EOQ for this component?
Annual demand is 12,000 units D=12,000
Ordering cost C = $25
Holding cost H(20% of the value of inventory)= ).20*2.5= $0.5
EOQ=
b) Reorder point
Lead time L = 5 days
Number of working days N= 250
ROP= ![]()
c) Cycle time
Cycle time T= (250)*1096/12000= 22.83 days in a cycle
d) Annual Holding cost = Q/2*h=1096/2*0.25*2.5= $274
Annual ordering cost = D/Q*C= 12000/1096*25= $273.72
e) Backorder cost (B) = $5
Minimum cost order quantity
EOQ=
f) Maximum number of backorders
S*= Q* x ![]()
g) Maximum inventory
Q*-S*= 1148.91-104.45 = 1044.46
h) Cycle time =250*1148.91/12000 = 23.94 days
i) Annual holding cost = (1148.91-104.45)2/(2*1148.91) *0.5= $237.38
Annual Ordering cost = 12000/1148.91 *25= $261.12
Backorder cost = 104.452/(2*1148.91) *5=$23.74
2. Wilson Publishing Company
a. Minimum cost production lot size
Setup cost = 150
Holding cost = 0.18*14.50
Usage Rate = 7200/250 = 29 units a day
Production (P) = 25000/250 = 100 units a day
Cost production lot size =
= 909.71×1.18 = 1073.45
Minimum cost production lot size (EPQ) = 1073.45
b. Number of production runs per year
7200/1073.45 = 6.7 times per year
c. Cycle time
1073.45/29 = 37.01 or 37 days
d. Length of a production run
1073.45/ 100 = 10.73 days
e. Maximum inventory
1073.45/100 x (100-29) = 762.14 units
f. Total annual cost
Annual holding cost= 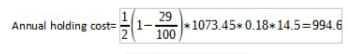
Annual ordering cost = 
Total cost= 994.6+1006.1=2000.7
g. Reorder point=d*Lead time
=(7200/250)*15= 285 units
Looking for Operation Management Assignment Help. Whatsapp us at +16469488918 or chat with our chat representative showing on lower right corner or order from here. You can also take help from our Live Assignment helper for any exam or live assignment related assistance.