Probability and Statistics- Mathematics Solved Homework Sample

QUESTION

 

Show enough of your work so that I will be able to tell how you arrived at your answers.

  1. Consider the probability distribution below.

x P(x)

10 0.1

20 0.2

30 0.3

40 0.3

50 0.1

  1. Calculate the probability that a randomly selected value of X will be less than 36.
  2. Calculate μ = E(X).
  3. Calculate σ2 = σ2(X).

 

2. Given that X has a binomial distribution with n = 10 and p = 0.30, find the following:

  1. the mean, μ 

  2. the variance, σ2. 

  3. P(X = 2) 

  1. Given that X has a Poisson distribution for which the average rate of occurrences is 0.04 per day and the length of the interval is 12 days, find the following:
    1. the mean of X 

    2. the variance of X 

  2. Assume that Y has an exponential distribution with λ = 4 per meter. Find . . .
    1. E(Y) 

    2. σ2(Y) 

  3. Suppose customers contact a health agency’s on-line help desk randomly and independently at an average rate of 6 per hour. Find . . .
  1. the average time between the beginning of one contact and the beginning of the next contact. 

  2. the average number of contacts in a 12-minute period. 

  3. the probability that there will be exactly two contacts between 4:00 and 4:12. 

  4. the probability that the length of time from now until the next contact will be more than 15 minutes. 


6. Find each of the following normal probabilities. Z has a standard normal distribution.

  1. P(Z < 1.86) 

  2. P(-0.73 < Z < 1.19) 


7.The time it takes an experienced installer to install a device in a customer’s home has a normal distribution with a mean of 52 minutes and a variance of 100 minutes2. The management wants to know the probability that an installation job will take more than one hour. Calculate this probability.

 

ANSWER

 

1.a)

 

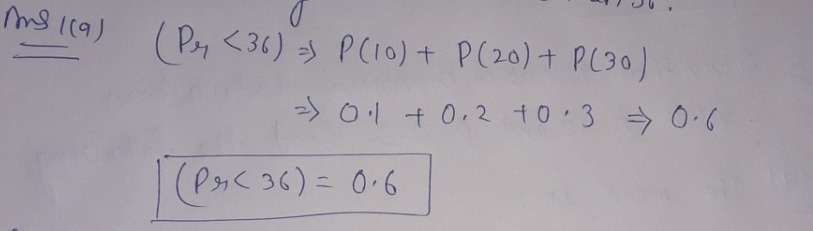
1.b)

 

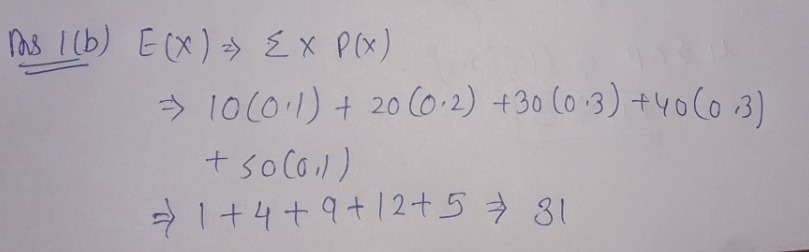
2.a)

 

2.b)

 

2.c)

 

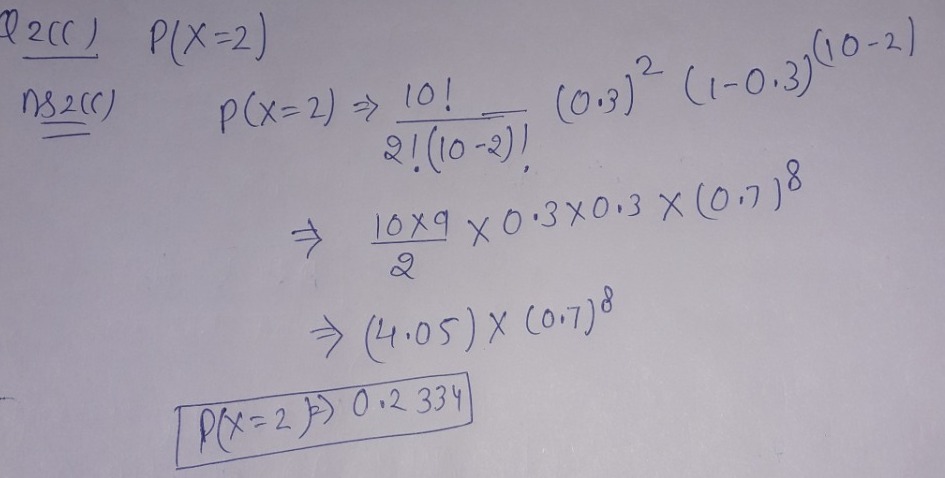
3.a)

 

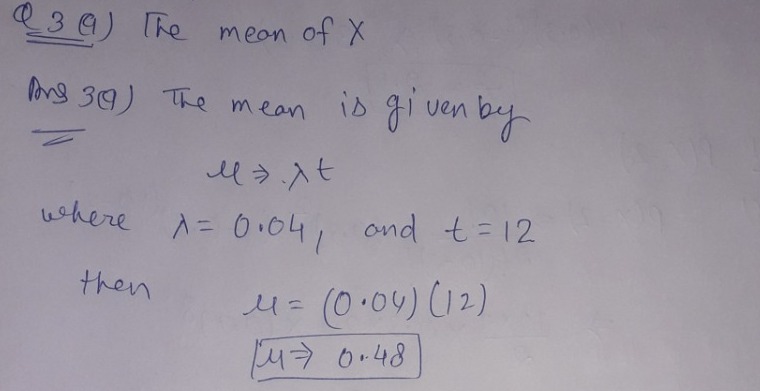
3.b)

 

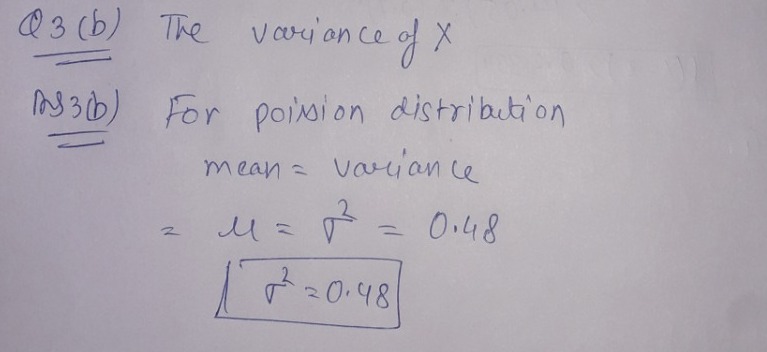
4.a,b)

 

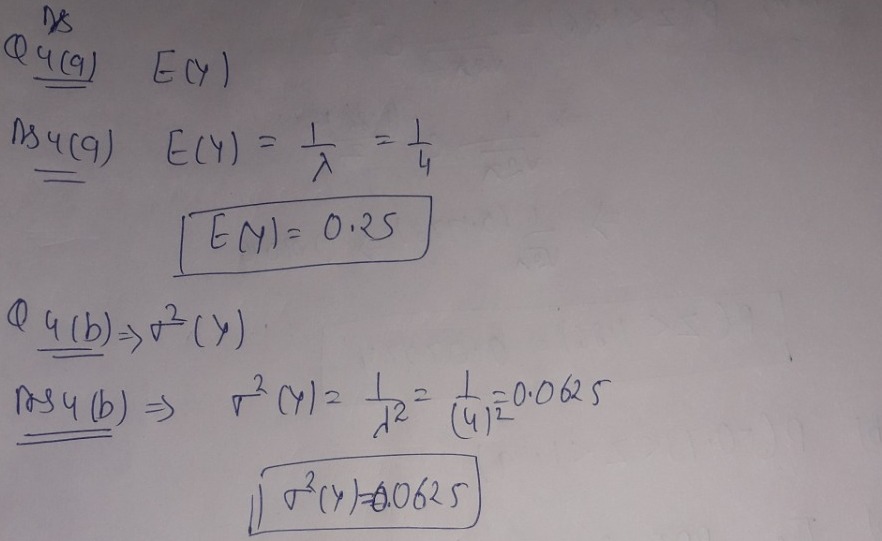
5.a)

 

5.b)

 

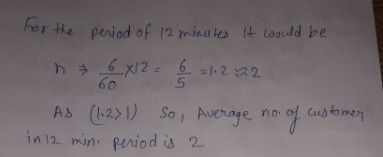
5.c)

 

5.d)

 

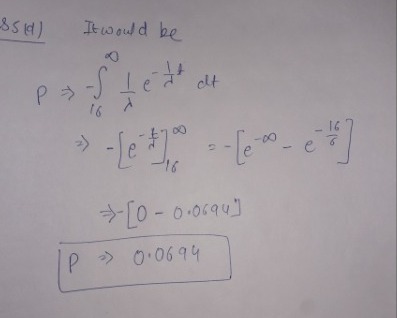
6.a)

 

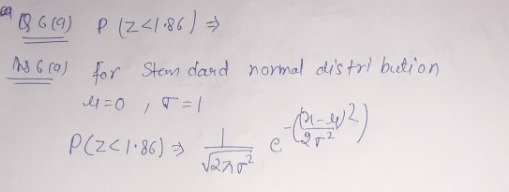
6.b)

 

7)

 

Looking for best Mathematics Assignment Help. Whatsapp us at +16469488918 or chat with our chat representative showing on lower right corner or order from here. You can also take help from our Live Assignment helper for any exam or live assignment related assistance.